墓地とゾンビの HashTable - Graveyard Hashing, Zombie Hashing

この記事は FOLIO Advent Calendar 2025 - Adventar 1日目です。

本記事では、Linear Probing をベースとした新しい HashTable の手法（Graveyard Hashing, Zombie Hashing）について解説します。

ベースにするのは

です。それぞれ2021年, 2025年ということで比較的新しい論文となります。

論文Bは某DB論文輪読会で取り扱われたものであり、本記事はそこで自分がわからなかった部分などをまとめたものになります。*1

長いのでなんとなくで良い方は性能比較の節だけ見ると良いと思います。

前提

本記事では Linear Probing と Robin Hood Hashing, Abseil (SwissTable) あたりについて大変ざっくりとした解説にとどめています。以下のような事前知識があるとより分かりやすいかもしれません。

Closed AddressingとOpen Addressing

HashTable の実装方式には大まかに Closed Addressing と Open Addressing があります。

Closed Addressing に分類される Chain 法では、Hash 衝突の際に連結リストをつくって要素をぶらさげていきます。 Open Addressing に分類される Linear Probing では、Hash 衝突の際に次スロットに要素をつめていきます。

（本記事で解説するような）ややこしいことにならないという点ではチェイン法が優勢となりますが、性能面でいうとキャッシュフレンドリーな Open Addressing の方に軍配があがることが多いです。

実際に、最近話題の高性能 HashTable 実装である

あたりも Open Addressing に分類されます。

今回紹介する Graveyard Hashing, Zombie Hashing も Open Addressing に分類されます。

注意

※ 上記の Abseil (Swiss Table), F14 は Open Addressing ではありますが Linear Probing ではありません。

じゃあ例に挙げるなよと思うかもしれませんがこれらのライブラリが Linear Probing を採用していない理由が今回の記事と関わってきます。

Load Factor

さて、これらの Hash Table ではできるだけ高速かつ省スペースな設計・実装が重要となりますが後者に関わるのが load factor(負荷率)です。

これは Hash の実装で使っている配列の何％まで要素を詰め込むか？という指標です。(しきい値をこれを超えたら大きな配列を作ってrehashする）

0.75をデフォルト値としている言語もあり概ねそのくらいが標準的な相場（もちろん物による）と言えそうですが、25%も配列のスロットが空いていますし、もう少し詰め込むことができればメモリ効率を改善することができそうです。

しかしあまりにも詰め込みすぎるとハッシュ衝突の確率が跳ね上がってしまい Get, Insert 等の性能が悪化してしまうことが懸念されます。

Linear Probing と Primary Clustering

Linear Probing では Hash 衝突の際に要素を次スロットに詰めていきます。

図にすると以下のイメージです。

※ hash値をh1, h2, ..とする

[x] <- h1の要素により占有
[ ] <- h1の要素を新たに入れようとした場合、本来の位置には入れられないのでここにinsertする

また衝突したキーは隣のスロットを占有することになるため、本来衝突していないはずのエントリも本来の場所に挿入できないことがあります。 上記の例で言えば h2 の要素を新たに挿入する際には（h2自体は衝突していないにも関わらず）、本来h2の要素を入れたい2個目のスロットではなく3個目のスロットを使うことになります。

こういった現象が重なるとどんどん肥大化したクラスタが形成されます。

下のような状況を考えるとさらにクラスタはどんどん大きくなっていくことが分かります。

[x] <- h1 の要素により占有
[x] <- h1 の要素により占有
[ ] <- 空きスロット（ここにh2が入ると前後のクラスタ同士が連結して巨大クラスタを形成）
[x] <- h3 の要素により占有
[x] <- h3 の要素により占有

問題となる空きスロットには h2 の要素だけでなく h1 の要素も入りうるため、空きスロットに囲まれた他のスロットより埋まりやすいといえます。もちろん他のキーも巻き込んだ大きな cluster がもっと前から続いていれば挿入される確率は何倍にもなります。

このような大きなクラスタを形成してしまう現象のことを Primary Clustering と呼び、Linear Probing の問題とされています。

この状況では要素の Hash 値を検索してからキーが一致する要素を見つけるまで何スロットも確認する必要があるので検索も挿入も遅くなってしまいます。

論文B 2.1によると load factor を 1 - 1/x とした場合の挿入コストが Θ(x2) になるそうです。なお x は空きスロット間の平均距離と捉えることができます。(from 論文B 2)

Primary Clustering による性能劣化を避けるために

  • Quadratic Probing（Linear Probing のようにN+1, N+2, N+3 と一つ隣のスロットに入れるのではなく N+1, N+2, N+4, N+9...と入れる先を徐々に遠くにしていく手法）
  • Double Hashing（衝突時に 2 つ目の hash 関数を使ってステップサイズを決定する手法）

などが用いられてきました。

Abseil や F14 が Linear Probing を採用していないのもこういった性能劣化を抑えたいという理由が大きそうです。

しかし、上記の手法では Linear Probing のメリットであるアクセスの局所性がいくぶん損なわれてしまいます。

Linear Probing のメリットを活かしながら高負荷状態でも高速な HashTable が欲しい。ということで生まれたのが Graveyard Hashing とその進化形である Zombie Hashing です。

ただしこの話に行く前にいくつか前提をお話します。

想定ワークロード

さきほどLinear Probingの問題点について述べましたが、これはもちろん負荷率が高い状況下での話です。（負荷率が低ければちゃんと良い性能になる。） そのため高負荷率での性質を考えたいわけですが、ただ insert され続けるだけだと配列が満杯になって挿入できなくなるだけなので insert と delete が同じくらい起こるようなワークロード を考えます。このようなワークロードのことをホバリングワークロードといいます。 （例：負荷率95%, 𝑥 ∈ [18,25] を維持するように insert, delete が繰り返される。）

本記事では計算量の厳密な議論についてはあまり触れませんが、時折引用する 𝑂(x) や Θ(x2) のようなオーダーについては上記のワークロードを想定したものとなります。

Linear Probing での削除操作

delete の方法について記載していなかったのですがここも重要になってくるので解説します。

Linear Probing では要素を単純に削除すると検索が上手く行えなくなります。

例えば

## 前提
key=x,y,zが全てhash値h1を持つとする

## before delete
[x] <- h1(key=x)の要素
[x] <- h1(key=y)の要素
[x] <- h1(key=z)の要素

## after delete (key=y)
[x] <- h1(key=x)の要素
[ ] <- （削除して空きスロットになった） 
[x] <- h1(key=z)の要素

といった状況を考えると GET(key=z) の操作がNOT_FOUNDを返してしまいます。（GETではkey=zのハッシュ値h1に対応する一つ目のスロットから順番に要素を比較していくのですが、空きスロットがある = 衝突して横にズレている可能性がないと判断して探索が打ち切られてしまうため）

これに対応する方法が２つあります。

Backward Shift Deletion

空きスロットがあるからいけないということは削除時に前詰めしてやれば良さそうです。

## 前提
key=x,y,zが全てhash値h1を持つとする

## before delete
[x] <- h1(key=x)の要素
[x] <- h1(key=y)の要素
[x] <- h1(key=z)の要素

## after delete (key=y)
[x] <- h1(key=x)の要素
[x] <- h1(key=z)の要素（削除時に前詰めする）
[] <- 空きスロット （h1(key=z)の要素が入っていたが前詰めの結果空きスロットになった）

これはこれで性能が出る（ Robin Hood hashing: backward shift deletion | Code Capsule ）ようですが削除時の（特に最悪ケースでの）コストはかなり上がってしまいます。(参考 https://15445.courses.cs.cmu.edu/fall2024/slides/07-hashtables.pdf#page=33）

Tombstone

要素をシフトさせる代わりの方法が tombstone （墓石）を置く方法です。削除済み要素を実際には削除せず削除マークをつける方式となります。

## 前提
key=x,y,zが全てhash値h1を持つとする

## before delete
[x] <- h1(key=x)の要素
[x] <- h1(key=y)の要素
[x] <- h1(key=z)の要素

## after delete (key=y)
[x] <- h1(key=x)の要素
[✝] <- 墓石
[x] <- h1(key=z)の要素

Getの際に墓石は埋まってるスロットとして扱い次の要素を更に探索するようにすればGet(key=z)に失敗することなく要素を探索することができます。 Insert の際は墓石に要素を入れてしまえばよいですが、Robin Hood Hashing (解説略）のように要素を本来の位置になるべく近づけるように並べるような方式を使っている場合は別途考慮が必要になったりします。（並べ替えておくと Insert コストが上がる代わりに Get 時にクラスタ末尾まで検索をかけずに途中で打ち切れるので早くなるメリットがあります。）

tombstone 形式の場合、スロットの状態は Empty, Used に加えて Tombstone という状態を取るようになります。(Get時に処理が変わるのでEmptyとしては使えない）

tombstone と性能

このように削除マーカーとして使える tombstone ですが、増えすぎると Get の性能がどんどん劣化してしまうため定期的な掃除（テーブル内の全ての tombstone を削除して empty と used のみで再構成する）が必要だとされていました。

tombstone 自体は単なる実装上のテクニックとして考えられていたようです。

(from 論文A Abstract) Interestingly, these design decisions, despite their remarkable effects, have historically been viewed as simply implementation-level engineering choices

ここまでが1960~1970年代ごろの出来事 （論文Aにて Tombstone に関して引用されている The Art of Computer Programming Volume 3 の first edition が 1973年刊行なのでおそらくそれよりも前に存在したはず。） です。

しかし、論文A にて tombstoneには単なる定期的な掃除ではなく、定期的に墓石を適切な位置に再配分することでクラスタ長の期待値を縮める事ができる と示唆されました。（突然指摘されたのか前の研究がずっと続いていたのかはよく調査できてないです。）

これは tombstone にanti clustering効果があることを利用したものです。

tombstone と anti clustering

前述したように Linear Probing では長く連続した占有区間（クラスター）ができると、さらに要素がそこに吸い寄せられてますます長くなる Primary Clustering が発生します。 これによりGet, Insertの双方が影響を受けますが tombstone を使うと Insert では tombstone のスロットに要素を挿入することができるため見かけ上、クラスタが分断されているように扱うことができます。（クラスタ内の tombstone により insert 先を探す探索距離が平均的に短くなる効果がある）

このような見かけ上のクラスタの分断のことを論文A,Bでは anti‑clustering 効果と呼んでいます。 tombstone の扱いの違いのため anti-clustering は Insert には効きますが Get には効きません。とはいえ、Robin Hood Hashing などの ordered linear probing を使っていれば（=要素が正規の位置に近い順にならんでいるなどクラスタ末尾まで検索しなくても途中で打ち切れるような条件が仮定できるなら） Get の探索コストは下げることができるので Insert 性能をケアできるのはとても重要な効果と言えます。

しかし tombstone は(delete がどこに発生するか分からない以上)ランダムに設定されることになり、分布が偏るとanti-clustering効果も期待できません。

そこで 論文A で提案されたのが Graveyard Hashing です。

Graveyard Hashing

従来の Tombstone 方式では tombstone の掃除を行うと配列の中は empty, used のどちらかだけになっていました。

Graveyard Hashingでは墓石を適切な位置に redistribute することで墓石の偏りを避け、anti-clustering効果を安定して発揮させるようにしています。

論文B Fig 2.

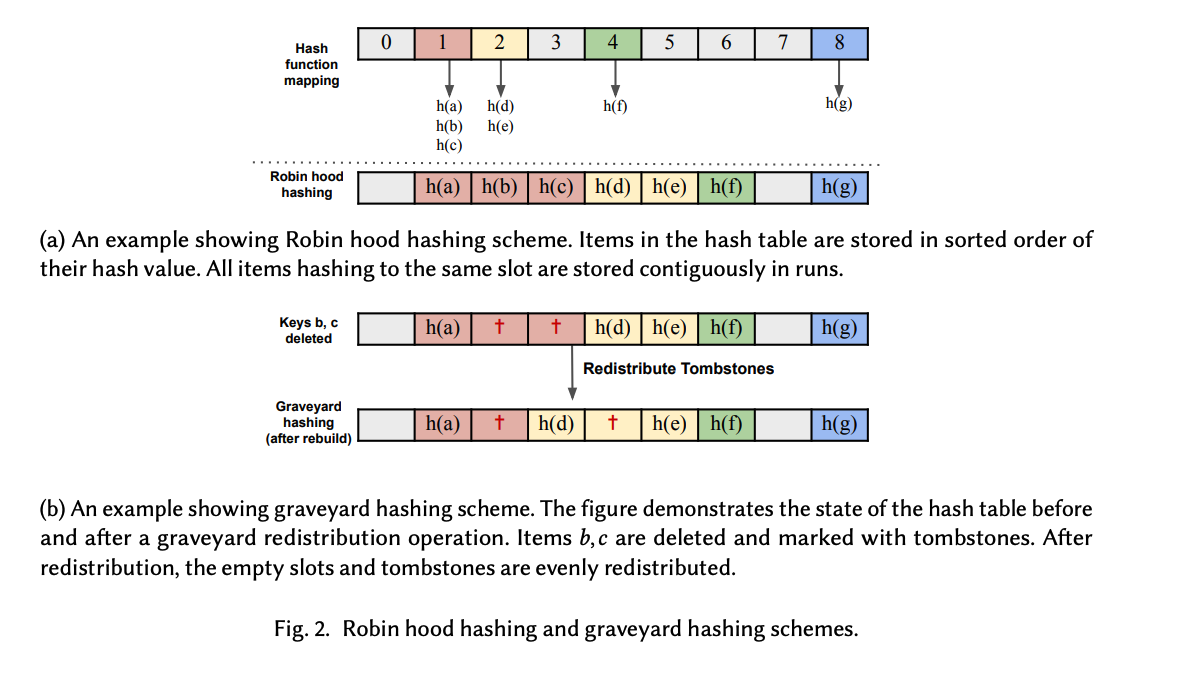
再構築について

tombstone の redistribute を行う再構築フェーズは以下のように行います。

  • 配列サイズ n のハッシュテーブルで負荷係数が 1-1/x の場合、n/(4x) 回の操作（挿入と削除）後に再構築を実行する
  • 再構築時には、n/(2x)個の墓石（primitive tombstoneという）が各ハッシュ値に均等に配置される。( { 2ix | i ∈ [n/(2x)]} )
  • それ以外の余分な tombstone がある場合は削除することで墓石の総数を制限する

Graveyard Hashing の計算量

Graveyard Hashingと通常の ordered linear probing の違いはなんとこれだけです。 (from 論文A. section 8)

これだけで hovering workload においても Insert/Delete/Lookup の全ての操作が Θ(𝑥) になります。また再構築にかかる時間は 𝑂(n) なので、挿入または削除ごとの償却時間は 𝑂(x) となります。

下表では他の方式は Θ(𝑥2) や Θ˜ (𝑥1.5) であることを考えると相当大きな差になります。

論文B Table 1.

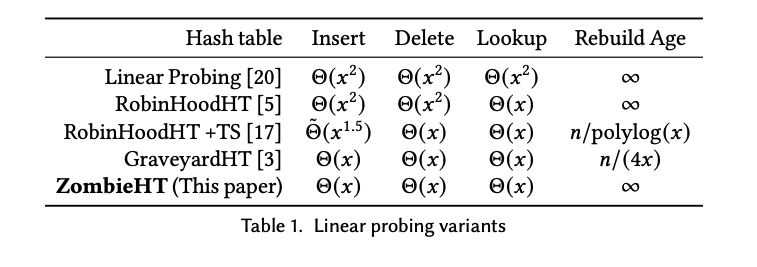
※ 論文A はこれらの操作に対する性能の解析を粛々と行うのが本旨なのでこの説明だとだいぶペラペラですが気になる人は論文A の section 8 をみてみましょう。

Graveyard Hashing の課題 - Zombie Hashing へ

さらっと書きましたが Graveyard Hashing では再構築フェーズがあるので 挿入・削除がO(x)であるというのは償却計算量の話になります。

償却計算量が O(x) なのは十分ありがたいのですが実応用しようとすると、insert 時に再構築フェーズが挟まる可能性があるため「たまにすごい遅い」という点が気になります。（つまりテールレイテンシーに課題がある。処理時間の分散が大きいとも言えます。）

実際、論文をみると紫色の Graveyard Hashibng は数回に一回スループットがガタ落ちしています。

論文B Fig 7.

一件ごとのレイテンシになおすと Graveyard Hashing では Insert の処理時間が 最小14.59 μs, 99.99% 52.18 μs と良好な性質を示していますが最大では 2173487.96 μs と4万倍もの時間がかかることが論文Bで指摘されています。実時間でも2secくらいなので結構気になりそうです。（図は後ほど紹介）

そこで 再構築フェーズでまとめて墓石を redistribute するのではなく操作のたびに少しずつやることで償却計算量で O(x) にするのではなく実際の計算量として O(x) になるよう deamortize してやりましょうというのが Zombie Hashing のアイデアです。

一回の操作でやることが増える分、単発のレイテンシは悪くなりそうですが最悪ケースの処理時間や処理時間の分散は小さくできそうです。

Simple deamortized Graveyard Hashing

一足飛びに Zombie Hashing の説明をする前に、simple版について見てみます。

まず insert, delete の度に全体を再構築するとものすごいコストが掛かってしまうので全体をいくつかの区間に分割してその限定された範囲のみ tombstone の再配布を行うことにしましょう。

  • ハッシュテーブル全体をR個のインターバル（区間）に分割する
  • insert または delete 操作のたびに単一のインターバルを再構築する
  • 再構築（ rebuild ） フェーズ
    • インターバル内の tombstone を以下のように再配置（tombstone の押し出し）
    • 次の primitive tombstone があるべき位置（c_p*x の間隔で設定。c_pは単なるパラメータ）に移動させる（すでにある場合は更に次の位置まで移動させる）
    • またはクラスタの終端まで移動させる

こうすることで insert/delete のたびに少しずつ墓石を再配置することができます。

※ パラメータc_pの値やインターバルのサイズ c_b * x を決める c_b の値については証明のところで値が取るべき条件が述べられていますが今回は省略しています。

しかしこの方式では再構築フェーズが O(x) で完了することを保証できません。 たとえば insert 時に primitive tombstone を挿入する場合、それより後方の要素をすべてずらす必要があります。この操作はインターバルの中で完結せず、空きスロット・別の tombstone に到達・クラスタの終端のいずれかまで到達する可能性があります。 また delete 時にも要素の前詰めが発生する可能性があり同様の問題を抱えます。

そもそも区間ごとにやるのが目的だったので操作が区間内で完結しないと片手落ちになってしまうということですね。

Zombie Hashing

それでは Zombie Hashing について仕組みを説明していきます

  • Hash テーブル全体をインターバルサイズ n/(c_p*x) に分割する
  • インターバルは最初から最後まで順に再構築される（最後の区間の再構築が終わったら最初に戻る）
  • 各 insert の後に１つのインターバルを再構築する
  • 再構築フェーズ
    • primitive tombstone がない場所に tombstone を配置する (すでに tombstone がある場合は何もしない）
    • 他のすべての tombstone を区間外に押し出す

再構築時の tombstone の押し出し方法が deamortized Graveyard Hashing と Zombie Hashing の唯一の違いです。

  • deamortized Graveyard Hashing は 不要な tombstone をクラスタの終端まで押し出します
  • Zombie Hashing は 不要な tombstone をクラスターの終端まで押し出すのではなく、次の再構築区間の先頭に押し出すだけです

※ なおこのとき次のインターバルまで押し出された tombstone を pushing tombstone と呼びます。

説明は上記なのですが、論文Bのセクション6.3や図4でもう少し詳細に記載があるので確認してみます。

が、その前に説明に必要な事柄を紹介します。

run と cluster の定義

今まで説明していた cluster だけだと概念が足りないので run という概念を導入します。

  • run: 同じハッシュ値を持つスロットの区間
  • cluster: 連続したrunの集まり（クラスタの先頭以外はすべて本来の位置にない要素が入っていることになる）

論文B figure. 3

quotienting

論文Bで性能比較などに利用されている実装は Quotienting を使っています。これは Hash 値をもつのではなくその fingerprint を持つ HashTable の形式を実現するテクニックです。 (正確にはそのままだと復元できなくなるので、復元できるようにしたものが Quotienting を 利用した HashTable となります。 復元できない場合は Bloom Filter などのように偽陽性を含むメンバーシップクエリに対応した Quotienting Filter になります。）

具体的には Hash 値 の上位 q bit を quotient, 残りを remainder と呼びます。 この場合、quotient を hashテーブルのindex として使うことができ、remainder のみを HashTable の中に保存することになります。

上図にある occupieds, runends などを使うとビットベクトルの rank/select 操作で高速に特定の quotient に紐づく run の開始、終了を検索できるといった技があるのですが簡潔データ構造の世界になってくるため説明は省略します。（図でいうと緑色に対応する quotient=4 に紐づく run は index 5 ~ 6 に入っているということがすぐ分かるようになります。）

後の rebuild 手順は quotienting を前提にしています。（この前提無しで下記手順を言い換えようとすると逆に長くなってしまいそうなので原文どおり quotienting を前提にした手順を述べます。）

詳細な rebuild 手順

少し前置きがありましたが改めて rebuild 手順です。

前提

  • テーブル全体を c_b * x に基づいて分割する
  • rebuild 対象の区間を [s, e) とする（s,e はそれぞれ区間の先頭と末尾の配列インデックス）

rebuild 手順

  • quotient s から開始する run を検索する。（なければ次の run を探す）
  • 各 i < e の quotient について以下を行う　
    • 𝑖 が primitive tombstone の位置の場合
      • pushing tombstone （前の区間から押し出された tombstone） があるなら run の先頭に一つだけ残す
      • なければ新しい tombstone を run の先頭に挿入する
    • run 内のすべての tombstone を run の外に押し出す。ただし次の run が空だったり、次のrunの quotient が 配列インデックスと等しい（正規の位置にある）場合は pushing tombstone を empty slot に変える
  • 次の run を見つけて処理を行う

論文B. Fig. 4

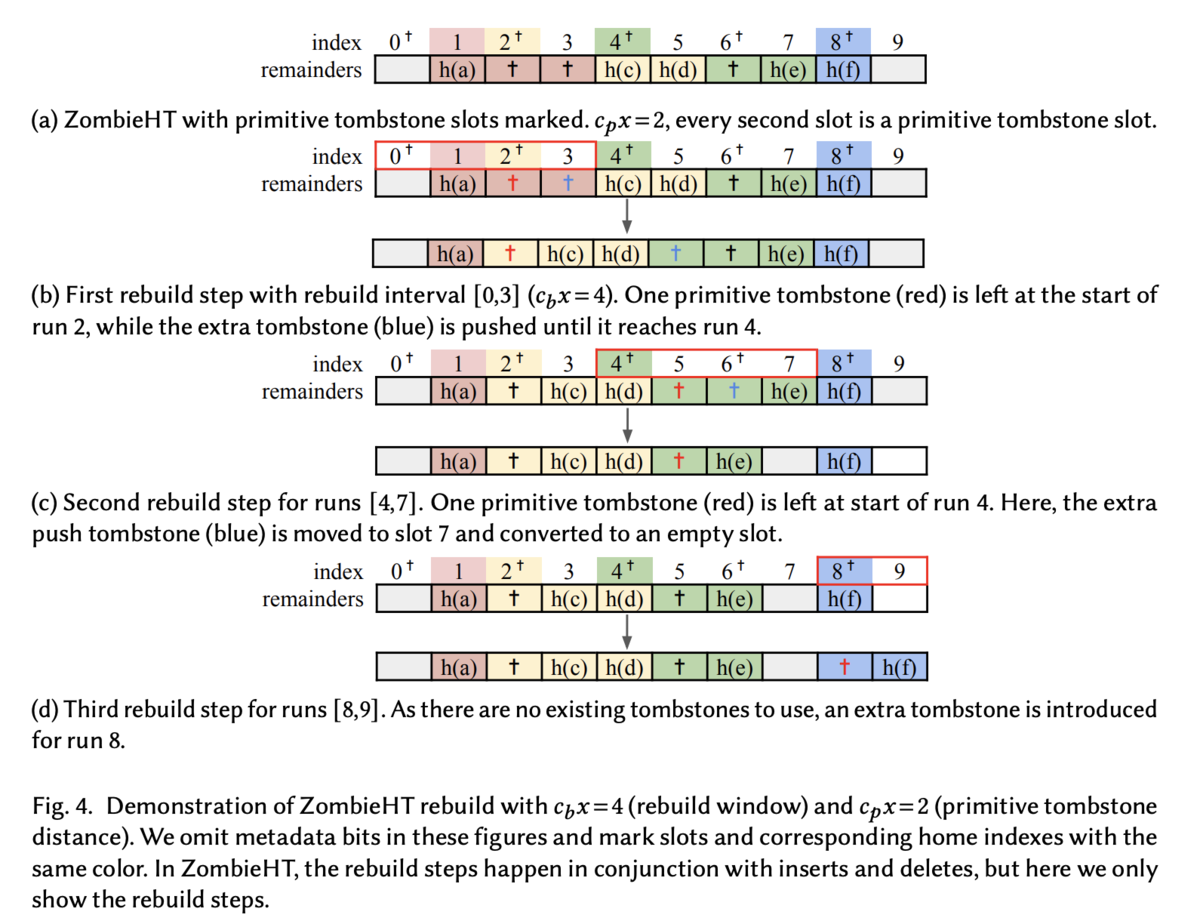
※ 上図を読み解く際は色が重要なので注意 (図の説明参照）

Zombie Hashing でやっていることは一見地味ですが、これによりすべての操作で最悪時 Θ(x) の時間計算量を保証することができます。償却時間計算量ではないため insert 後に再構築が走って時間がかかるといった Graveyard Hashing にあった問題を解消することができます。

論文では Optimized 版として primitive stoneを新たに insert するのではなく delete 時に導入された tombstone のみを使って再配布を行う ZombieHTDelete の解説も行われています。ざっくり説明すると tombstone が有用か不要かを判断するロジックを持って tombstone が新たに発生した場合に適切な位置に配置するかクリアするかを決定するロジックになっています。こちらのほうがアクセスするデータの局所性や負荷率が改善されるようです。

バリエーション

論文B では Robin Hood Hashing ベースでの実装だけでなく Abseil のように SIMD に対応させて一度に複数要素を照合する ZombieHT(V) も提案されています。

  • ZombieHT(C): Ordered。Robin Hood Hashingベース
  • ZombieHT(V): Unorderd。ベクトル命令対応版

なお上記を含めた様々なバリエーションの実装として、論文Bの著者による実装 GitHub: saltsystemslab/ZombieHT が公開されています。 Quotient Filterベースの実装になっていて読み解くにはその解説も必要になるのですが今回は省略するため詳細については論文Bを参照してください。

性能比較

ベンチマークの結果としては以下になります。左側が ordered, 右側が unordered になります。

論文B Table 5.

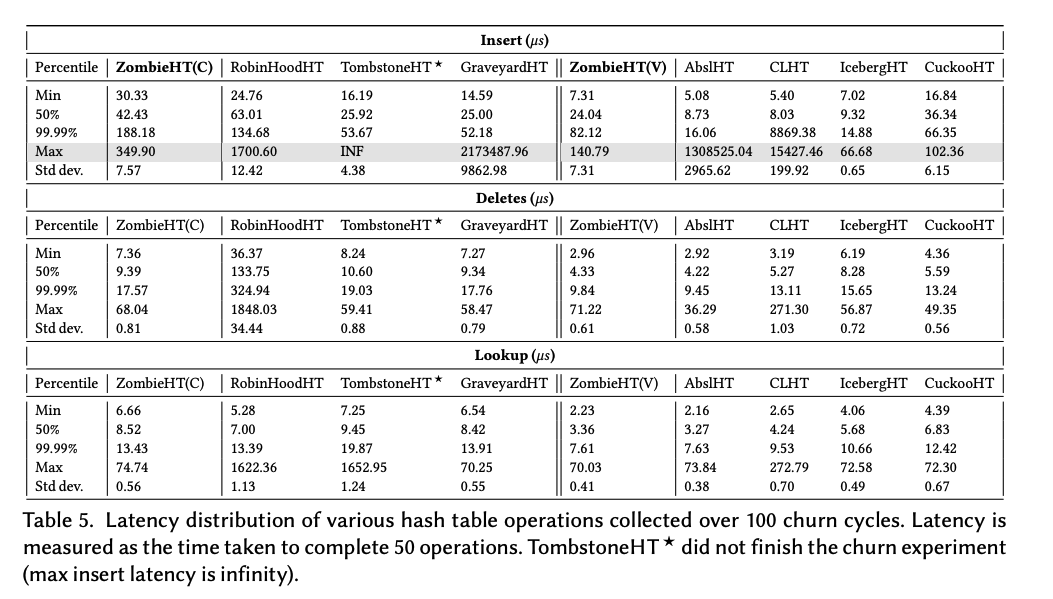
注目してほしいのは灰色になっている Insert の最大レイテンシです。

GraveyardHT の 2173487.96 μs (≒ 2sec) が ZombieHT(C) だと 349.90 μs まで改善しています。 99.99%の値が3~4倍になっている点はあるものの2秒止まるよりは良いと言えるワークロードは多そうです。

SIMD版の ZombieHT(V) についても同様に最大値を抑えることに成功しています。

なお、みんな大好き Abseil についても（このベンチマークの条件下では）レイテンシの最大値が大きくなることがこの表から分かります。 Abseil は tombstone 込みの load factor 87.5%が超えた場合に tombstone の数が 3/32 を超えていたら tombstone を掃除, そうでない場合は裏側の配列サイズを2倍にする (しきい値は経験則で決定されたもの）という設計になっているようで、まとめて掃除をするという操作がこの性能特性を引き起こすようです。

※ 注意: 当然ながら、実際のワークロードが違えば結果も変わるはずなので、あくまで一例として見てください。

IcebergHT について

また、この表を見ると IcebergHT の優秀さが目につきますが空間効率を考えると話が変わってきます。(ZombieHT(V) が 70.55% に対して IcebergHT が 62.71% の空間効率)

論文B Table 6.

なお IcebergHTは Iceberg Hashing: Optimizing Many Hash-Table Criteria at Once(2021) や IcebergHT: High Performance PMEM Hash Tables Through Stability and Low Associativity にて提案された手法で、こちらでは高い空間効率が主張されています。 IcebergHTは動的リサイズ対応（配列が埋まってきたら全体を一気に grow するのではなく少しずつ成長させる。）・参照安定性あり（リサイズ以外で要素の位置が変わらない）な HashTable になっていて、 Graveyard Hashing, Zombie Hashing とは満たす機能が変わっているので、色々な機能を満たしている状態でこの空間効率が達成されているので一概に上図だけを見て判断するのは危険だったりします。

特に動的リサイズについては本記事で紹介したテールレイテンシー増加の原因にもなるので（hovering workload だと発生しないですが）、重要なところかと思います。（なお今回は省略していますが論文Aには Graveyard Hashing における動的リサイズについても記載されていますので興味がある人はそちらもご参照ください。）

終わりに

長かったですが以上となります。論文1,2ともに単にアルゴリズムの提案だけでなく計算量の解析・証明まで行っていますが本記事ではほとんど紹介していません。 amortized版で計算量を下げる改善をして、deamortizedするという流れは PFDS の流れに近いなという感覚があり、やや懐かしい気持ちになりました。

Zombie Hashing の今後の実応用も気になるところですが、実務上のパフォーマンスがどうかというのはそもそも想定しているワークロード次第といった別の難しさもあると思いますし、今後の検証・発展等に期待したいところです。

宣伝

株式会社FOLIO では immutable な HashTable を使うことが多いですが mutable な HashTable に興味がある人もぜひカジュアル面談に申し込んで HashTableについて 会社の雰囲気やキャリアについて話しましょう！

カジュアル面談（社員紹介専用フォーム/社員紹介の方のみこちらからご応募下さい） - 株式会社FOLIO

参考文献

*1:もうちょっと参加したいんですが仕事と育児の両立の難しさを感じる今日この頃